sgroupbion.blogg.se - Repeating fibonacci sequence formula

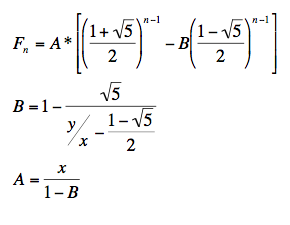
True or False: At any generation, there are always more immature rabbits than mature rabbits.

How many pairs of breeding rabbits are there at the 8th generation? How many pairs of immature rabbits are there at the 8th generation? How many pairs of rabbits are there at the 8th generation? There are many more levels of self-similarity throughout the family tree. For example, starting at generation 3, the left branch resembles the whole family tree, and starting at generation 4 the right branch Note the fractal structure of the family tree. The number of rabbit pairs in a given generation is the sum of the number of rabbit pairs in the previous two generations. The process continues like this, and the family tree grows with the total number of rabbits at a given generation being a number in theįibonacci Sequence. Generation, the first pair produces another pair, and the second pair is old enough that it also produces another pair, and now there are five pairs. At the third generation, the rabbits can breed, and they produce a new pair, so there are now two pairs of rabbits.Īt the fourth generation, the first pair produces another pair, while the second pair is still too young to reproduce, so there are now three pairs. Starting at the top, at the first generation (or iteration), there is one pair of newborn rabbits, but it is too young to breed. Each point represents a pair of rabbits, not a single individual.Įmpty dots represent immature rabbit pairs, while filled dots represent mature rabbit pairs capable of breeding. The image below charts the development of the rabbit family tree, moving from top to bottom.

A pair of rabbits will produce a litter of one male and one female rabbit (obviously oversimplified).

Rabbits must mature two months before they can breed, after which they breed once per month.

Imagine that the rules for rabbit reproduction are simplified to these: Consider the breeding of rabbits, a famously fertile species. Let's see how Fibonacci Numbers can show up in some natural patterns. where F n is the Fibonacci number for the given iteration n. There are infinitely many Fibonacci numbers, and they rapidly get very large.Įtc. You can keep repeating this simple process forever. The next number in the sequence is 3 + 2 = 5. Just add the current number ( 2) to the one before it ( 1), resulting in 3. To make the next number in the sequence, you Start with the numbers 1 and 1, and add them together. (Although the number sequence was also used in Sanskrit poetry as early as 450 BC). As one of the examples in his book, he described the sequence of numbers that would come to be calledįibonacci Numbers. The use of Arabic numerals into Europe, which would replace Roman numerals. This book was significant in the history of mathematics because it introduced He published a book in the year 1202 under the pen-name 'Fibonacci'. Like family trees and actual trees, we'll see Fibonacci numbers in the periods of the bulbs of the Mandelbrot Set fractal, and we'll see how the Fibonacci sequence relates to the Golden Ratio,Įven before Leonardo da Vinci was exploring the fractal nature of rivers, trees and blood vessels, another Leonardo - named Leonardo of Pisa - was exploring fractal We'll find Fibonacci numbers in natural processes Optimizing the timing between reviews (spaced repetition) can increase your retention and save you valuable time.In this chapter, we will learn about the arithmetic fractal of the Fibonacci Sequence, and see how it shows up in many systems.

Memory science has shown that the “curve of forgetting” is steeper when you first learn something but becomes shallower with each timely review. Total Recall – Dynamic Spaced Repetition LearningĪchieve total recall through spaced repetition The formulas are smart, meaning that your level of recall (how difficult or easy it was to recall) factors into the calculation of the next review date. I used Fibonacci's number sequence in my formula to fit this better for students who may only have a limited number of weeks before next exam. I've seen a decent number of spaced repetition templates out there, but most are generally geared for longer periods of learning. Hello all! I've published a new template for those of us who have to cram a lot of information into our brains in not a lot of time (🧠🔨).